
Um Z-Score é um valor estatístico que informa quantos desvios padrão um valor específico está da média de todo o conjunto de dados. Você pode usar as fórmulas MÉDIA e DESVPAD.S ou DESVPAD.P para calcular a média e o desvio padrão dos seus dados e, em seguida, usar esses resultados para determinar o Z-Score de cada valor.
O que é um Z-Score e o que as funções MÉDIA, DESVPAD.S e DESVPAD.P fazem?
Um Z-Score é uma maneira simples de comparar valores de dois conjuntos de dados diferentes. É definido como o número de desvios-padrão da média em que um ponto de dados está. A fórmula geral é assim:
=(DataPoint-AVERAGE(DataSet))/STDEV(DataSet)
Aqui está um exemplo para ajudar a esclarecer. Digamos que você queira comparar os resultados dos testes de dois alunos de álgebra ensinados por professores diferentes. Você sabe que o primeiro aluno obteve 95% no exame final em uma turma e o aluno na outra turma obteve 87%.
À primeira vista, a nota de 95% é mais impressionante, mas e se o professor da segunda turma fizesse um exame mais difícil? Você pode calcular o Z-Score da pontuação de cada aluno com base nas pontuações médias em cada classe e no desvio padrão das pontuações em cada classe. Comparar os Z-Scores dos dois alunos pode revelar que o aluno com 87% de pontuação foi melhor em comparação com o restante da turma do que o aluno com 98% de pontuação em comparação com o restante da turma.
O primeiro valor estatístico necessário é a “média” e a função “MÉDIA” do Excel calcula esse valor. Ele simplesmente adiciona todos os valores em um intervalo de células e divide essa soma pelo número de células que contêm valores numéricos (ignora as células em branco).
O outro valor estatístico de que precisamos é o “desvio padrão” e o Excel tem duas funções diferentes para calcular o desvio padrão de maneiras ligeiramente diferentes.
As versões anteriores do Excel tinham apenas a função “DESVPAD”, que calcula o desvio padrão enquanto trata os dados como uma “amostra” de uma população. O Excel 2010 dividiu isso em duas funções que calculam o desvio padrão:
- DESVPAD.S: Esta função é idêntica à função “DESVPAD” anterior. Ele calcula o desvio padrão enquanto trata os dados como uma “amostra” de uma população. Uma amostra de uma população pode ser algo como os mosquitos específicos coletados para um projeto de pesquisa ou carros que foram retirados e usados para testes de segurança em colisões.
- STDEV.P: Esta função calcula o desvio padrão enquanto trata os dados como toda a população. Uma população inteira seria algo como todos os mosquitos da Terra ou todos os carros na produção de um modelo específico.
O que você escolhe é baseado no seu conjunto de dados. A diferença será geralmente pequena, mas o resultado da função “DESVPAD.P” será sempre menor que o resultado da função “DESVPAD.S” para o mesmo conjunto de dados. É uma abordagem mais conservadora supor que há mais variabilidade nos dados.
Vamos ver um exemplo
No nosso exemplo, temos duas colunas (“Valores” e “Z-Score”) e três células “auxiliares” para armazenar os resultados das funções “MÉDIA”, “DESVPAD.S” e “DESVPAD.P”. A coluna “Valores” contém dez números aleatórios centralizados em torno de 500, e a coluna “Z-Score” é onde calcularemos o Z-Score usando os resultados armazenados nas células 'auxiliares'.

Primeiro, calcularemos a média dos valores usando a função “MÉDIA”. Selecione a célula onde você armazenará o resultado da função “MÉDIA”.

Digite a seguinte fórmula e pressione entrar -ou- use o menu “Fórmulas”.
=AVERAGE(E2:E13)
Para acessar a função através do menu “Fórmulas”, selecione o menu suspenso “Mais funções”, selecione a opção “Estatística” e clique em “MÉDIA”.
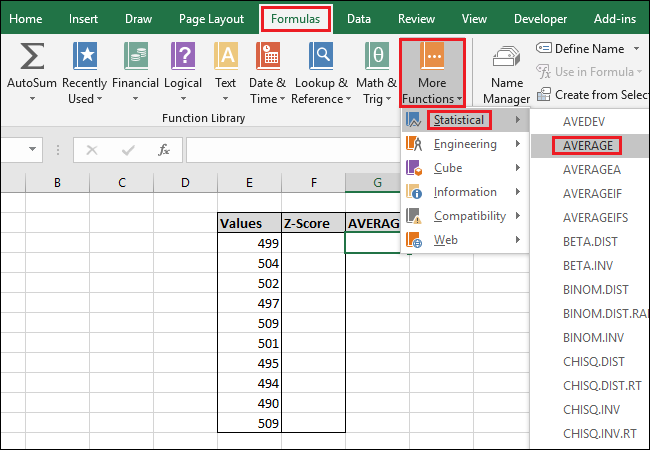
Na janela Argumentos da Função, selecione todas as células na coluna “Valores” como entrada para o campo “Número1”. Você não precisa se preocupar com o campo “Número2”.

Agora pressione “OK”.

Em seguida, precisamos calcular o desvio padrão dos valores usando a função “DESVPAD.S” ou “DESVPAD.P”. Neste exemplo, mostraremos como calcular os dois valores, começando com “DESVPAD.S”. Selecione a célula onde o resultado será armazenado.

Para calcular o desvio padrão usando a função “DESVPAD.S”, digite esta fórmula e pressione Enter (ou acesse-o através do menu “Fórmulas”).
=STDEV.S(E3:E12)
Para acessar a função através do menu “Fórmulas”, selecione o menu suspenso “Mais funções”, selecione a opção “Estatística”, role um pouco para baixo e clique no comando “DESVPAD.S”.

Na janela Argumentos da Função, selecione todas as células na coluna “Valores” como entrada para o campo “Número1”. Você também não precisa se preocupar com o campo “Número2” aqui.
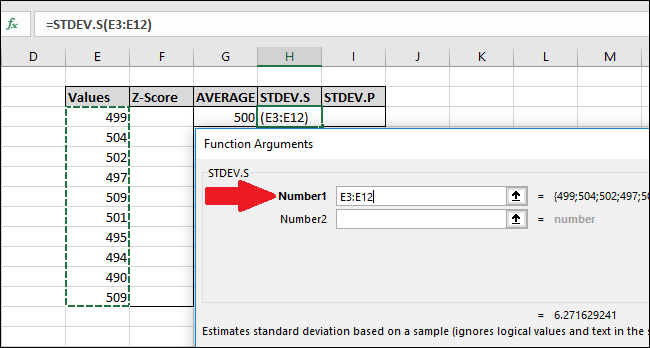
Agora pressione “OK”.

A seguir, calcularemos o desvio padrão usando a função “DESVPAD.P”. Selecione a célula onde o resultado será armazenado.

Para calcular o desvio padrão usando a função “DESVPAD.P”, digite esta fórmula e pressione Enter (ou acesse-o através do menu “Fórmulas”).
= DESVPAD.P (E3: E12)
Para acessar a função através do menu “Fórmulas”, selecione o menu suspenso “Mais funções”, selecione a opção “Estatística”, role um pouco para baixo e clique na fórmula “STDEV.P”.

Na janela Argumentos da Função, selecione todas as células na coluna “Valores” como entrada para o campo “Número1”. Novamente, você não precisa se preocupar com o campo “Número2”.

Agora pressione “OK”.

Agora que calculamos a média e o desvio padrão de nossos dados, temos tudo o que precisamos para calcular o Z-Score. Podemos usar uma fórmula simples que faça referência às células que contêm os resultados das funções “MÉDIA” e “DESVPAD.S” ou “DESVPAD.P”.
Selecione a primeira célula na coluna “Z-Score”. Usaremos o resultado da função “DESVPAD.S” para este exemplo, mas você também pode usar o resultado de “DESVPAD.P”.

Digite a seguinte fórmula e pressione Enter:
=(E3-$G$3)/$H$3
Como alternativa, você pode usar as seguintes etapas para inserir a fórmula em vez de digitar:
- Clique na célula F3 e digite
=( - Selecione a célula E3. (Você pode pressionar o tecla de seta esquerda uma vez ou use o mouse)
- Digite o sinal de menos
- - Selecione a célula G3 e pressione F4 para adicionar os caracteres “$” para fazer uma referência “absoluta” à célula (ela passará por “G3”> “$G$3 “>” G$3 ″> “$G3 ″> “G3” se você continuar pressionando F4)
- Tipo
)/ - Selecione a célula H3 (ou I3 se você estiver usando “DESVPAD.P”) e pressione F4 para adicionar os dois caracteres “$”.
- pressione Enter

O Z-Score foi calculado para o primeiro valor. É 0,15945 desvios padrão abaixo da média. Para verificar os resultados, você pode multiplicar o desvio padrão por este resultado (6,271629 * -0,15945) e verificar se o resultado é igual à diferença entre o valor e a média (499-500). Ambos os resultados são iguais, portanto o valor faz sentido.

Vamos calcular a pontuação Z do restante dos valores. Destaque toda a coluna 'Z-Score' começando com a célula que contém a fórmula.
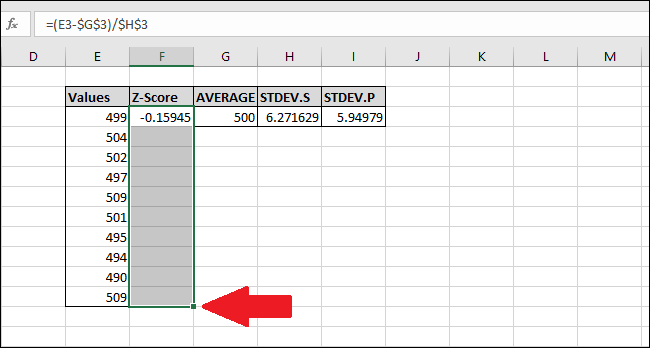
Pressione Ctrl + D, que copia a fórmula na célula superior para baixo através de todas as outras células selecionadas.

Agora, a fórmula foi “preenchida” para todas as células, e cada uma sempre fará referência às células “MÉDIA” e “DESVPAD.S” ou “DESVPAD.P” corretas devido aos caracteres “$”. Se você receber erros, volte e verifique se os caracteres “$” estão incluídos na fórmula inserida.
Cálculo do Z-Score sem usar células 'Helper'
As células auxiliares armazenam um resultado, como as que armazenam os resultados das funções “MÉDIA”, “DESVPAD.S” e “DESVPAD.P”. Eles podem ser úteis, mas nem sempre são necessários. Você pode ignorá-las completamente ao calcular um Z-Score usando as seguintes fórmulas generalizadas.
Aqui está um usando a função “DESVPAD.S”:
=(Value-AVERAGE(Values))/STDEV.S(Values)
E um usando a função “STEV.P”:
=(Value-AVERAGE(Values))/STDEV.P(Values)
Ao inserir os intervalos de células para os “Valores” nas funções, certifique-se de adicionar referências absolutas (“$” usando F4) para que, quando você 'preencher', não estiver calculando a média ou o desvio padrão de um intervalo diferente de células em todas as fórmulas.
Se você tiver um conjunto de dados grande, pode ser mais eficiente usar células auxiliares porque não calcula o resultado das funções “MÉDIA” e “DESVPAD.S” ou “DESVPAD.P” a cada vez, economizando recursos do processador e acelerando o tempo necessário para calcular os resultados.
Além disso, “$ G $ 3” leva menos bytes para armazenar e menos RAM para carregar do que “MÉDIA ($ E $ 3: $ E $ 12).”. Isso é importante porque a versão padrão de 32 bits do Excel é limitada a 2 GB de RAM (a versão de 64 bits não tem limitações quanto à quantidade de RAM que pode ser usada).
0 Comments